데이터 스케일링 (Data Scaling), 어떤 스케일러를 쓸 것인가?

데이터를 모델링하기 전에는 반드시 스케일링 과정을 거쳐야 한다.

특히 k-means 등 거리-기반의 모델에서는 넓은 범위의 값을 가지는 변수가 거리 측도를 지배하는 상황을 방지하기 위해 스케일링이 매우 중요하다.

스케일링 개념

데이터 스케일링(Data Scaling)

데이터의 값의 범위를 조정하는 것, 데이터 수치를 일정한 수준으로 변환하는 것

왜?

ex) 키(height)와 몸무게(weight) 변수가 있다고 하면 단위는 각각 (cm, kg)이며 표본이 성인이라고 가정하면 범위는 (150cm - 190cm), (40kg - 100kg) 정도로 다른 단위가 범위를 가진다. 이러한 단위 차이는 몇몇 회귀 모형이나 머신러닝 기법에서 문제를 일으킬 수 있다.

거리 기반의 모델링(distance based model)을 수행할 때 상대적으로 범위가 넓은 몸무게 변수가 거리 계산을 하는 과정에서 더 많은 기여를 하게 되어 더 중요한 변수 or 영향력이 높은 변수로 인식될 수 있다.

=> 따라서, 이러한 문제를 방지하기위한 방법 중 하나로 범위를 재정의하는 스케일링를 수행한다.

- 서로 다른 Features의 평균과 분산, 최대, 최소값이 모두 다르면 이를 비교하기 어렵고 AI 학습 성능이 저하

- 단위나 범위를 일정하게 변환하여 데이터들 간 이질성을 보완

- 데이터를 비교 가능한 척도로 변환

- 데이터의 값이 크거나, 작은 경우에 모델 알고리즘 학습과정에서 0으로 수렴하거나 무한으로 발산하는 것을 방지하거나, 예측 값이 범위를 벗어나는 입력데이터의 값(Outlier)에 더 큰 영향을 받는 것을 방지한다.

=> 표준화(Standardization), 정규화(Normalization)

“언제 정규화를 하고 언제 표준화를 할까?”

명확한 답은 없다. 통상적으로는 표준화를 통해 이상치를 제거하고, 정규화를 통해 상대적 크기에 대한 영향력을 줄인다.

예를 들어, cluster analysis에서 특정 거리 측도를 기반으로 피처 간의 유사성을 비교하기 위해 표준화가 중요할 수도 있다. 또 다른 예로, 주성분 분석(Principal Component Analysis)에서도 분산을 극대화하는 특성에 관심이 있기 때문에 일반적으로 표준화를 선호한다. 정규화는 pixel intensities를 특정 범위(RGB 색상 범위의 경우 0~255) 내에 맞추기 위해 이미지 프로세싱에서 주로 사용된다.

스케일링이 필요한 경우

1. 주성분 분석(PCA)

: 높은 분산/ 넓은 범위를 가지는 변수는 낮은 분산을 가지는 변수보다 주성분에서 큰 회귀계수를 가지게 된다. 즉, 중요하지 않은 변수도 범위가 넓으면 주성분에서 중요한 변수로 간주

2. 군집(clustering)

: 거리-기반 알고리즘으로 거리 측도(ex. 유클리디안, 맨하튼 ... )를 이용하여 관측값 사이에서 유사성을 찾아 군집을 형성한다. 따라서, 넓은 범위를 가지는 변수는 군집에서 더 큰 영향력을 가진다.

3. k-최근접 이웃(knn)

: k-최근접 이웃은 거리-기반 알고리즘으로 새로운 관측값의 주변에 있는 k개의 이웃(데이터)를 이용하여 유사성 측도에 기반해 관측값을 분류한다. 따라서, 유사성 측도에 모든 변수가 동일하게 기여할 수 있도록 스케일링을 수행해야한다.

4. 서포트벡터머신(SVM)

: 서포트벡터 머신은 서포트벡터와 분류기(hyperplane) 사이 거리인 마진(margin)을 최대로 만들어주는 분류기를 찾는 알고리즘이다. 따라서, 특성 값이 크면 거리를 계산할 때 다른 특성보다 우선시 되어 영향력을 많이 미치게 된다.

5. 회귀모델에서 변수 중요도를 측정하기 전

: 예측을 위한 회귀 모델링이 목적이라면 표준화를 수행할 필요가 없지만, 변수의 중요도나 다른 회귀계수들과 비교를 하는 것이 목적이라면 표준화가 수행된 독립변수를 이용하여 회귀 모형을 피팅하여 표준화된 계수의 절대값을 비교하여 회귀 분석에서의 변수 중요도를 측정할 수 있다.

6. LASSO/RIDGE 회귀 전

: 각 변수에 관련된 계수의 크기에 패널티를 부여하며, 변수의 규모는 계수에 적용되는 패널티 정도에 영향을 미친다. 분산이 큰 변수의 계수는 작아 불이익을 덜 받는다. 따라서 구 회귀를 모두 맞추려면 표준화가 필요하다.

스케일링이 필요하지 않은 경우

로지스틱 회귀, 트리 기반 모델(ex. 의사결정나무, 랜덤 포레스트 ...), 그래디언트 부스팅은 변수의 크기에 민감하지 않으므로 표준화를 수행해줄 필요가 없다.

회귀분석에서 조건수

함수의 조건수(condition number)는 인자에서 작은 변화의 비율에 대해 함수가 얼마나 크게 변하는지에 대한 인자 측정치이다. 조건수가 크면 약간의 오차만 있어도 해가 다른 값을 갖게 되며, 조건수가 크면 회귀 분석을 사용한 예측값도 오차가 커지게 된다.

[변수들의 단위 차이가 있는 경우] : 스케일링

[상관관계가 큰 독립 변수들이 있는 경우] : 변수 선택/PCA(차원축소) 등으로 해결

[독립 변수, 종속 변수가 심하게 한쪽으로 치우친 분포] : 로그/제곱근 함수를 사용하여 변환된 변수를 사용하면 회귀 성능이 향상됨

scikit-learn에서는 스케일링을 수행하는 다양한 스케일러를 제공한다.

모든 스케일러는 다음과 같은 메소드를 갖는다.

SCALER.fit()
- 데이터 변환을 학습
- train data set 에서만
SCALER.transform()
- 실제로 데이터 변환을 수행
- train/test data set 모두에게 적용

스케일링 종류

cikit-learn에서는 MinMaxScaler, MaxAbsScaler, StandardScaler, RobustScaler등을 제공한다.

preprocessing.MinMaxScaler() : 최대/최소값이 각각 0과 1 사이에 위치하도록 스케일링
preprocessing.MaxAbsScaler() : 데이터가 -1과 1 사이에 위치하도록 스케일링
preprocessing.StandardScaler() : 기본 스케일, 데이터의 평균 = 0, 분산 = 1이 되도록 스케일링
preprocessing.RobustScaler() : 데이터의 중앙값(median) = 0, IQE(interquartile range) = 1이 되도록 아웃라이어의 영향을 최소화
preprocessing.LabelEncoder() : 0과 n_classes - 1 사이의 값으로 대상 레이블을 인코딩
preprocessing.OneHotEncoder() : categorical features을 원-핫 숫자 배열로 인코딩
preprocessing.Normalizer() : 샘플을 개별적으로 단위 표준으로 정규화

데이터의 분포 별로 각각의 스케일링 결과는 아래와 같다.

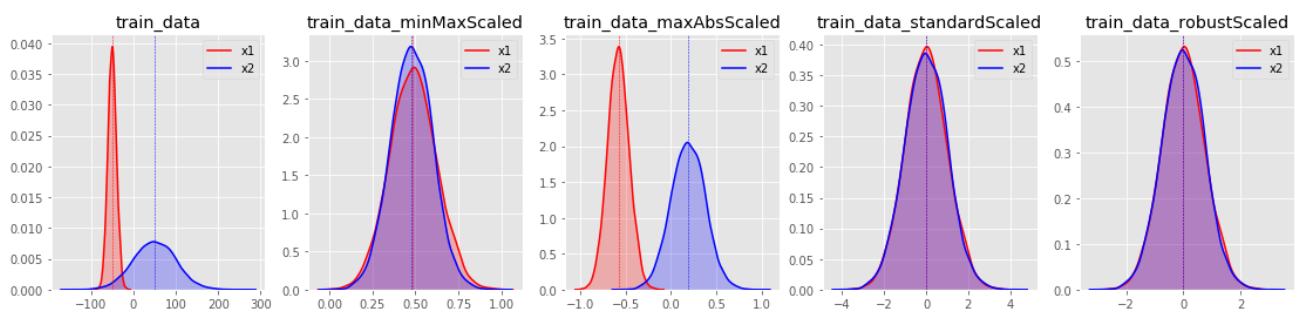
변환 분포를 살펴보면 StandardScaler와 RobustScaler의 변환된 결과가 대부분 표준화된 유사 형태의 데이터 분포로 반환되는 것을 확인할 수 있다.

StandardScaler(표준화) vs Normalization(정규화)

정규화는 값의 범위를 [0, 1]로 옮긴다. 그래서 데이터의 컬럼들이 평등하게 0과 1사이에 놓여지기 때문에 학습할 때 어느 컬럼에 중점을 두고 학습하기보다는 평등하게 보고 학습시킨다.

표준화는 데이터를 정규분포(종모양 분포)를 따르게 한다. 즉, 평균을 0, 표준편차는 1이 되도록 만들어준다.

정규화는 데이터를 0과 1사이로 범위를 정하게 하고, 표준화는 0을 중심으로 퍼진다고 생각하면 된다.

1. StandardScaler, Z-core, 표준화

- 기존 변수에 범위를 정규 분포로 변환

- (x - x의 평균값) / (x의 표준편차)

- 데이터의 최소, 최대 값을 모를 경우 사용

각 피처의 평균을 0, 분산을 1로 변경한다. 즉 데이터가 표준 정규 분포(standard normal distribution)를 따르도록 스케일링

모든 feature들이 같은 스케일을 갖는다.

평균을 제거하고 데이터를 단위 분산으로 조정한다. 그러나 이상치가 있다면 평균과 표준편차에 영향을 미쳐 변환된 데이터의 확산은 매우 달라지게 된다. 이상치가 있는 경우 균형 잡힌 척도를 보장할 수 없다.

평균과 표준편차가 이상치로부터 영향을 많이 받는다는 점에서 이상치에 민감

from sklearn.preprocessing import StandardScaler

# standard scaler 선언 및 학습
standardScaler = StandardScaler().fit(X_train)

# train셋 내 feature들에 대하여 standard scaling 수행
X_train_standard = standardScaler.transform(X_train)

# test셋 내 feature들에 대하여 standard scaling 수행
X_test_standard = standardScaler.transform(X_test)

2. MinMaxScaler (Normalization)

- 데이터를 0-1사이의 값으로 변환

- (x - x의 최소값) / (x의 최대값 - x의 최소값)

- 데이터의 최소, 최대 값을 알 경우 사용

모든 feature가 0과 1 사이에 위치하도록 스케일링. (default, 최소값 = 0, 최대값 = 1 )

식 : (x - x의 최소값) / (x의 최대값 - x의 최소값)

단점 : 이상치가 존재할 경우, 변환 결과가 매우 좁은 범위로 압축될 수 있음.(이상치(Outlier)의 존재에 민감)

from sklearn.preprocessing import MinMaxScaler

# minmax scaler 선언 및 학습
minmaxScaler = MinMaxScaler().fit(X_train)

# train셋 내 feature들에 대하여 minmax scaling 수행
X_train_minmax = minmaxScaler.transform(X_train) 

# test셋 내 feature들에 대하여 minmax scaling 수행
X_test_minmax = minmaxScaler.transform(X_test)

3. MaxAbsScaler

최대 절대값과 0이 각 1, 0이 되도록 하여 양수 데이터로만 구성되게 스케일링

데이터가 -1과 1 사이에 위치하도록 스케일링( 절대값의 최소값 = 0, 절대값의 최대값 = 1 )

데이터의 값이 양수만 존재할 경우 MinMaxScaler와 유사하게 동작

이상치가 큰 쪽에 존재할 경우 민감

from sklearn.preprocessing import MaxAbsScaler

# MaxAbsScaler 선언 및 학습
maxabsScaler = MaxAbsScaler().fit(X_train)

# train셋 내 feature들에 대하여 maxabs scaling 수행
X_train_maxabs = maxabsScaler.transform(X_train)

# test셋 내 feature들에 대하여 maxabs scaling 수행
X_test_maxabs = maxabsScaler.transform(X_test)

4. RobustScaler

- StandardScaler에 의한 표준화보다 동일한 값을 더 넓게 분포

- 이상치(outlier)를 포함하는 데이터를 표준화하는 경우(영향을 최소화)

데이터의 중앙값(median) = 0, IQE(interquartile range) = 1이 되도록 스케일링

RobustScaler를 사용할 경우 StandardScaler에 비해 스케일링 결과가 더 넓은 범위로 분포

모든 feature들이 같은 스케일

이상치의 영향 최소화

from sklearn.preprocessing import RobustScaler

# RobustScaler 선언 및 학습
robustScaler = RobustScaler().fit(X_train)

# train셋 내 feature들에 대하여 robust scaling 수행
X_train_robust = robustScaler.transform(X_train)

# test셋 내 feature들에 대하여 robust scaling 수행
X_test_robust = robustScaler.transform(X_test)

참고

- https://lucian-blog.tistory.com/106

- https://bskyvision.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EB%8D%B0%EC%9D%B4%ED%84%B0-%EC%A0%84%EC%B2%98%EB%A6%AC-%EC%A0%95%EA%B7%9C%ED%99%94normalization%EC%99%80-%ED%91%9C%EC%A4%80%ED%99%94standardization

- https://www.analyticsvidhya.com/blog/2020/04/feature-scaling-machine-learning-normalization-standardization/

- https://medium.com/greyatom/why-how-and-when-to-scale-your-features-4b30ab09db5e

- https://builtin.com/data-science/when-and-why-standardize-your-data

- https://syj9700.tistory.com/56

- https://ebbnflow.tistory.com/137

- https://mkjjo.github.io/python/2019/01/10/scaler.html

- https://scikit-learn.org/stable/modules/classes.html#module-sklearn.preprocessing

- https://cheris8.github.io/data%20analysis/DP-Data-Scaling/#minmaxscaler